A kutatás az instabilitás lefolyásának nemlineáris vizsgálatát alapul véve a modellezés kérdésére koncentrál. Ez a szakirodalom posztlokalizációnak nevezett jelenség során játszik fontos szerepet. A vizsgálatot általában a véges elem módszerrel numerikusan végzik. Ennek során azonban gyakran felmerül az a probléma, hogy a számított eredmények, így például a lokalizációs zóna mérete, függenek a felvett elemek méreteitől. A probléma okát abban találtuk meg, hogy a kontinuumot leíró egyenletrendszerek szinguláris tulajdonságokat mutatnak. Abban az esetben viszont, hogyha a kontinuumot nemlineáris dinamikai rendszernek tekintve a lokalizáció jelensége statikus bifurkációnak értelmezzük, lehetőség van a posztlokalizációnak a bifurkációelmélet módszereit felhasználó vizsgálatára. Ez a megközelítés előnyös, mert az analitikus módszer lehetővé teszi a szinguláris viselkedés okának megtalálását, illetve a jelenségről alkotott modell pontosítását.
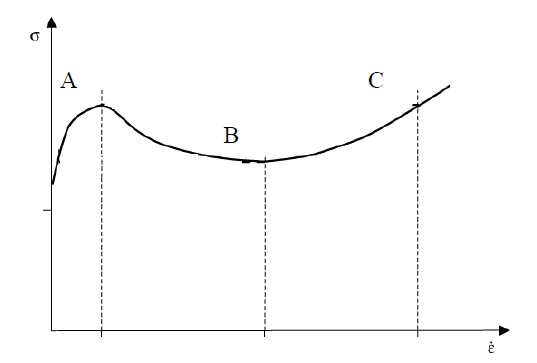
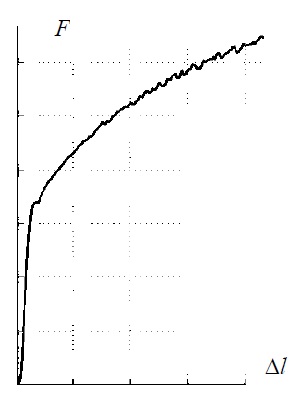
A kutatás fontosabb eredményei két témában jelentkeztek: a Portevin-Le Chatelier hatás értelmezése és a gradiens(-függő) anyagmodellek vizsgálata. Az 1920-as években publikált dolgozataikban Portevin és Le Chatelier leírták, hogy bizonyos ötvözetek szakítóvizsgálatánál egyes esetekben öngerjesztett rezgés lépett fel, egyenletes húzás mellett a szakítódiagramként nem sima függvény adódott. Megmutattuk, hogy lehetséges a Portevin-Le Chatelier hatást dinamikus anyagi instabilitásként értelmezni. A kutatás másik része a gradiens(-függő) anyagmodellek vizsgálata. Az ilyen anyagokat alkalmaztunk az erek egyszerű biomechanikai modellezéseiben egyfajta mechanikai megokolását adva a belgyógyászati, illetve szemészeti szakorvosi gyakorlatban alapvető szemfenéki érvizsgálatának.
Kutatásaink fontos eredménye a dinamikai rendszerek stabilitási kritériumainak a variációs elvekhez kapcsolható alkalmazási lehetőségeinek vizsgálata. Ezen a területen a szilárd kontinuumok feltételes variációs elv felhasználásával történő modellezésére adtunk példát az anyag stabilitásának feltételezése mellett (pl. Drucker posztulátum). Az anyagmodellezésben egyszerre szerepeltetjük a feltételes Lagrange deriváltat és (a dinamikai rendszerek körében használt) Ljapunov stabilitás feltételét.
